Varlıkların en ve boylarındaki değişim; yüzey alanı, kesit alanı ve hacimlerinde değişmeye neden olur.
oranı varlıkların dayanıklılığını belirler. Bu oranın büyük olması, dayanıklılığın fazla olduğu anlamına gelir.Bu oranın küçük olması da dayanıklılığın küçük olduğu anlamına gelir.
Sonuç olarak dayanıklılık,
Buna göre, silindir, küp ve dikdörtgenler prizması şeklindeki düzgün kesit alanlı cisimlerin dayanıklılığını bulabilmek için oturtulduğu yüzey ve hacim değerine bakarak oranlama yapmak gerekir.
Dayanıklılık - Boyut İlişkisi
Varlıklar orantılı olarak büyütüldüğünde dayanıklılıkları azalır mı? Bu arada o varlığı oluşturan kütle artacağı için varlığın ağırlığı da dayanıklılığı etkiler mi? Acaba dayanıklılık ile ağırlık artışı orantılı mıdır? Varlıklar orantılı olarak büyütüldüğünde dayanıklılıkları ağırlıklarına oranla daha az mı artar? Şimdi bu soruların cevaplarını arayalım.
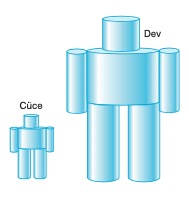
Bunun için boyutları çok küçük olan bir cüceyi şekildeki gibi modelleyelim.
Daha sonra bu cücenin 10 kat büyültüldüğünü düşünelim.
Tüm vücudu bacaklar taşıdığı için kesit alanı olarak bacakların toplam ke-sit alanı alınır. Cüce ve devin dayanıklılıkları için toplam hacimleri hesaplanır. Kesit alanları toplam hacme oranlandığında cüce ile devin dayanıklılıkları kıyaslanmış olur.
Gerekli hesaplamalar yapılarak, cücenin ebatlarının orantılı biçimde 10 kat artırılması durumunda kesit alanı / hacim oranı 10 kat azalır. Bu da daya-nıklılığının 10 kat azaldığı anlamına gelir. Bir cismin dayanıklılığı, boyut değiştirme oranı ile ters orantılıdır. Dolayısıyla varlıkların ebatları orantılı bir şekilde artırıldığında dayanıklılıkları varlık üzerinde olumsuz etki eder.
Varlıkların ebatları küçükken dayanıklılıkları büyük olurken, ebatları büyütüldüğünde dayanıklılıkları küçük olur. Sonuç olarak, cisimlerin ebatları (üç boyutu) orantılı bir şekilde hangi oranda artırılırsa, dayanıklılıkları o oranda azalır. Cisimlerin ebatları orantılı bir şekilde azaltıldığında ise dayanıklılıkları o oranda artar.
Günlük hayatta, varlıkların ebatlarının dayanıklılık ile ilişkisini gösteren birçok örneğe rastlarız. Bir karınca kendi ağırlığının birkaç katını rahatlıkla kaldırabilir-ken, karıncayı orantılı bir şekilde insan kadar büyütecek olursak bu büyüklükte kendi ağırlığını bile taşıyamayacak duruma gelir.Benzer olarak bir sinek uçak kadar büyütülse, değil havada uçmak, hareket bile edemez. Çünkü büyültme sırasında ağırlığı dayanıklılığından daha çok artar. Ve kendi ağırlığını taşıyamaz duruma gelir.
 |
 |
 |
2019-12-02 Admin Admin
Taglar: Dayanıklılık
| Dayanıklılık, Yüzey Gerilimi ve Kılcallık - İlginizi çekebilecek başlıklar |
|---|
|
Adezyon ve Kohezyon Kuvveti
Daha önceleri sıvılar ve gazlar incelenirken yalnız ağırlık kuvvetlerinin etkisi altındaki özellikleri incelendi. Bu incelemeler yapılırken akışkanlar ideal olarak kabul edildi. Aslında hiç bir akışkan ideal değildir. |
|
Aurora Nedir? Aurora Nasıl Oluşur?
Gökyüzündeki doğal ışık görüntüleri olan auroralar, genelde gece çıplak gözle de izlenebilir. Bu doğa olayını bir bütün olarak görebilmek için, oluşma zamanlarında uzaydan bakmak gerekir. |
|
Fizikte Kılcallık Olayı
Kılcal boru adı verilen çok küçük çaplı borularda suyun yükselmesi bilinen bir olaydır. Bitki özsuyunun ağaçlarda yükselmesi kısmen kılcallık etkisi iledir. Su, kayalardaki yarık ve çatlaklardan yukarı doğru tırmanır ve donduğu zam |
|
Düzgün Geometrik Cisimlerin Kesit Alanı, Yüzey Alanı ve Hacimlerinin Hesaplanması
Küp, Prizma, Slindir, Küre Kesit Alanı, Yüzey Alanı ve Hacimlerinin Hesaplanması |
Sayfa Yorumları