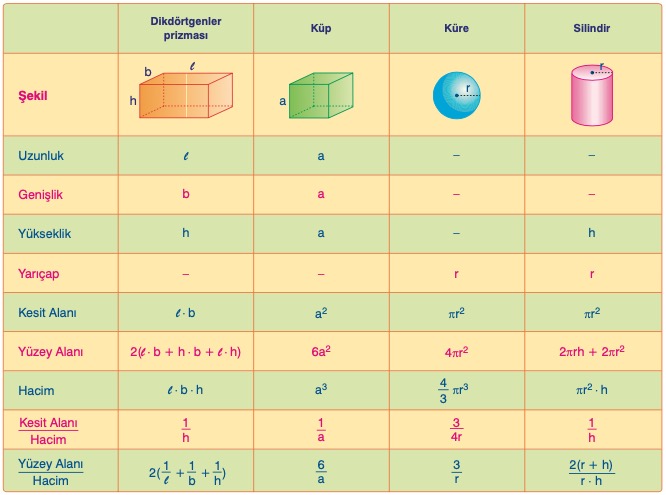
Düzgün Geometrik Cisimlerin Kesit Alanı, Yüzey Alanı ve Hacimlerinin Hesaplanması

Küp

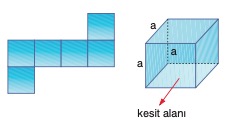
Küp şeklindeki bir cismin şekli ve yüzey alanının açılımı şekildeki gibidir. Küpün her kenarının uzunluğu a kadar olduğuna göre,
Kesit Alanı: S_A = a² dir.

Küpün aynı yüzeyinden 6 tane olduğundan ve her bir yüzeyin alanı a² ol-duğundan toplam yüzey alanı bir yüzey alanın 6 katı olur.
Yüzey Alanı: Y_A = 6a² dir.

Küpün hacmi üç boyutun çarpımı ile bulunur.
Hacim: V = a³ tür.

Prizma

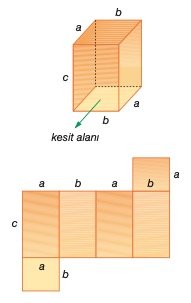
Boyutları şekildeki gibi verilen ve a, b kenarı üzerinde duran prizmanın ke-sit alanı,
Kesit Alanı: S_A = a b dir.

Prizmada farklı üç yüzey alanı vardır. Açılımı şekildeki gibi olan prizmanın farklı yüzey alanından ikişer tane vardır.
Yüzey Alanı: Y_A = 2(a b + a c + b c) dir.

Farklı üç boyutun çarpımı hacmi verir.
Hacim: V = a b c dir.

Silindir

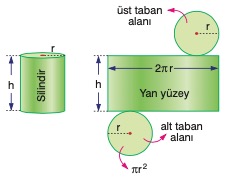
Yarıçapı r olan silindirin kesit alanı daire olduğundan,
Kesit Alanı: S_A = π r² dir.

Silindirin toplam yüzey alanı, daire biçimli taban ve tavan iki alan ile yan yü-zey alanın toplamından bulunur.
Yüzey Alanı: Y_A = 2π r² + 2π r h dir.

Silindirin hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
Hacim: V = π r² h dir.

Küre

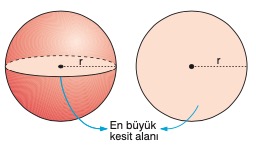
r yarıçaplı kürenin merkezinden geçecek şekilde kestiğimizde, daire şeklinde en büyük kesit alanını elde ederiz.

Kesit Alanı: S_A = π r² dir.

Yüzey Alanı: Y_A = 4π r² dir.

Hacim: V = (4 / 3) π r³ dir.

** Küre; aynı hacimdeki geometrik cisimler arasında yüzey alanı en kü-çük olan cisimdir.

Boyuttaki Değişmeler: Büyültme ve Küçültmeler

Büyültme ve küçültmeler sırasında boyutlardaki değişmelerde varlıkların kesit alanlarının, yüzey alanlarının, hacimlerinin ve kütlelerinin nasıl etkilen-diğini detaylıca inceleyelim.

Varlıkların uzunluk, genişlik ve yükseklik gibi boyutlarında yapılacak büyült-me ya da küçültmelerde kesit alanları, yüzey alanları, hacimleri ve kütlele-rinin nasıl değiştiğini, aşağıdaki gibi kenar uzunlukları 1 cm, kütlesi 1 g olan küp biçimli bir cisim üzerinde inceleyelim.

Birim küpün kesit alanı, yüzey alanı, hacmi ve kütlesi ile bu küpün her bir kenarı 2 katına ve 3 katına uzatıldığındaki kesit alanı, yüzey alanı, hacmi ve kütlesi aşağıdaki gibi değişir.

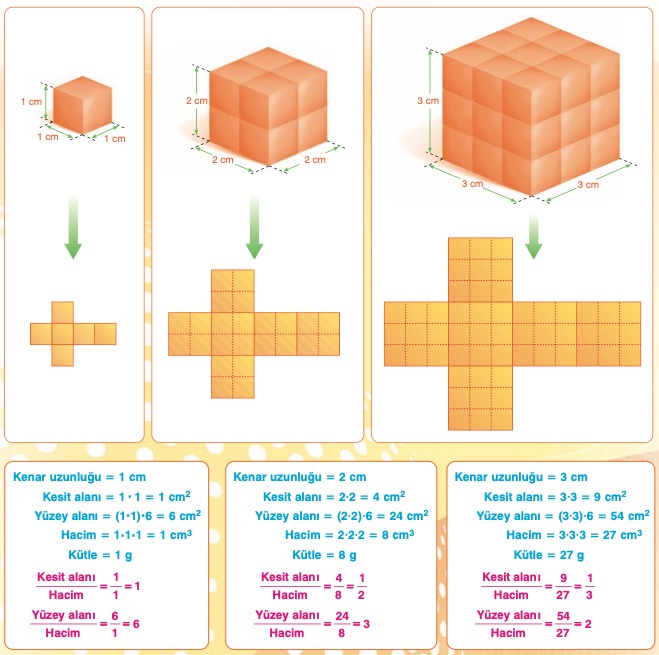
Sonuç olarak:

* Bir cismin boyutları hangi oranda değişirse kesit alanı bu oranın karesi kadar değişir.

* Bir cismin boyutları hangi oranda değişirse hacmi bu oranın küpü kadar değişir.

* Bir cismin boyutları hangi oranda değişirse kütlesi ve ağırlığı bu oranın küpü kadar değişir.

* Bir cismin boyutları büyürken kesit alanındaki artışın, hacmindeki artışa oranı azalır.

* Bir cismin boyutları hangi oranda değişirse yüzey alanı bu oranın karesi kadar değişir.

* Bir cismin boyutları büyürken yüzey alanındaki artışın, hacmindeki artışa oranı azalır.

2019-12-01 Admin Admin

Taglar: Düzgün Geometrik Cisimlerin Kesit Alanı Yüzey Alanı Hacimlerinin Hesaplanması

Dayanıklılık, Yüzey Gerilimi ve Kılcallık - İlginizi çekebilecek başlıklar
Adezyon ve Kohezyon Kuvveti Daha önceleri sıvılar ve gazlar incelenirken yalnız ağırlık kuvvetlerinin etkisi altındaki özellikleri incelendi. Bu incelemeler yapılırken akışkanlar ideal olarak kabul edildi. Aslında hiç bir akışkan ideal değildir.
Aurora Nedir? Aurora Nasıl Oluşur? Gökyüzündeki doğal ışık görüntüleri olan auroralar, genelde gece çıplak gözle de izlenebilir. Bu doğa olayını bir bütün olarak görebilmek için, oluşma zamanlarında uzaydan bakmak gerekir.
Dayanıklılık Gerekli hesaplamalar yapılarak, cücenin ebatlarının orantılı biçimde 10 kat artırılması durumunda kesit alanı / hacim oranı 10 kat azalır. Bu da daya-nıklılığının 10 kat azaldığı anlamına gelir. Bir cismin dayanıklılığı, boyut